Locret: 개인 장치에서 장문 맥락 추론을 가능하게 하다
2024/09 황우상 @칭화대학교 & 홍콩과기대학교 [中文][English][にほんご]
요약: 우리는 Locret를 소개합니다. 이는 분할 예비 채우기와 캐시 추방을 활용하는 경량의 훈련 기반 KV 캐시 압축 방법입니다. Locret는 Phi-3-mini-128K 및 Llama-3.1-8B-instruct에 대해 각각 전체 캐시 대비 $20\times$ 및 $8\times$ KV 캐시 압축 비율을 달성하며, 1시간 미만의 GPU 훈련만을 요구합니다. Locret는 견고하며 여러 효율적인 추론 방법과 호환됩니다. 우리가 알기로는, Locret는 Llama-3.1-8B 또는 이와 유사한 모델을 단일 Nvidia 4090 GPU에서 배포할 수 있는 최초의 프레임워크로, 128K 장문 맥락 추론을 품질 손실 없이 구현하며 최소한의 시스템 최적화를 요구합니다.
배경
소비자용 장치, 엔드사이드 LLM, 및 장문 맥락 추론
최근 몇 년 동안 대규모 언어 모델(LLM)의 개발이 급속히 확장되는 것을 목격했습니다. 이 모델들은 거의 모든 분야에서 성능이 향상되고 있으며, 개발자들은 이제 소비자용 장치를 위해 특별히 설계된 더 작고 효율적인 모델을 만드는 데 집중하고 있습니다.
소비자용 장치. LLM의 사용자 경험을 개선하기 위해 하드웨어 제조업체들은 더 저렴하고 작은 GPU를 설계하고 생산하거나, GPU와 NPU를 단일 SoC에 통합하여 AI 모델의 전체 비용을 절감하고 있습니다. 예를 들어, Nvidia 4090은 24GB의 GPU 메모리만 가지고도 개인 컴퓨터에 설치할 수 있으며, 가격은 2000달러 미만으로 유지되고 있습니다. 애플과 퀄컴 같은 회사들도 행렬 곱셈이나 희소 연산과 같은 AI 컴퓨팅 작업에 최적화된 장치를 만들고 있습니다. 하지만 이 장치들은 여전히 제한된 GPU 메모리와 계산 성능에서 어려움을 겪고 있습니다.
엔드사이드 LLM. 메모리와 계산 제약을 극복하기 위해 엔드사이드 LLM은 사용자 장치에서 효율적인 AI 서비스를 제공하도록 설계되고 훈련되었습니다. 이러한 모델은 일반적으로 8B 미만의 크기이며, 보통 1B에서 3B 사이의 매개변수를 가집니다. MiniCPM은 1.2B에서 4B 범위의 모델을 포함하고 있으며, Phi-3-mini는 약 3B, Llama-3.2 시리즈는 1B 및 3B 모델이 있습니다. 크기가 줄어들었음에도 불구하고, 이 LLM은 7B-8B 모델에 버금가는 인상적인 성능을 자주 보여줍니다. 다중 홉 추론, 짚 속의 바늘 찾기, AI 기반 운영 시스템과 같은 더 복잡한 작업을 지원하기 위해, 이러한 모델은 종종 확장된 맥락 길이를 처리할 수 있도록 설계됩니다. MiniCPM-3-4B는 최대 32K 토큰을 처리할 수 있으며, Phi-3-mini-128K와 Llama-3.2-1B/3B는 128K 장문 맥락 추론을 지원하여 엔드사이드 LLM이 장문 맥락 작업을 효과적으로 수행할 수 있도록 합니다.
장문 맥락 추론. 장문 맥락 LLM 추론은 전통적인 단문 맥락 추론과 두 가지 주요 방식에서 다릅니다:
-
주의 메커니즘에 대한 계산 오버헤드 증가
맥락 길이가 길어질수록, 주의 점수를 계산하는 데 필요한 계산량이 기하급수적으로 증가하여 각 트랜스포머 블록 내에서 계산 예산의 큰 부분을 소비합니다.
-
키-값(KV) 캐싱에 대한 더 높은 메모리 요구
더 긴 맥락은 더 큰 KV 캐시를 필요로 하며, 이는 최대 메모리 사용량을 크게 증가시킵니다.
이러한 도전 과제는 장문 맥락 LLM 추론에 대한 계산 비용을 줄이고 메모리를 더 효율적으로 관리할 수 있는 혁신적인 기술을 필요로 합니다. 소비자용 장치의 제한된 메모리로는 그러한 캐시를 완전히 지원할 수 없기 때문에, 이러한 장치에서 장문 맥락 추론을 위해 KV 캐시 압축 알고리즘을 개발하는 것이 매우 중요합니다.
기존의 효율적인 추론 접근법
KV 캐시는 종종 추론 처리량의 병목이 되므로, 여러 가지 KV 캐시 중심의 효율적인 추론 알고리즘이 개발되었습니다. 우리는 이를 알고리즘 최적화와 시스템 최적화로 분류합니다.
알고리즘 최적화:
-
양자화 기반 방법:
KV 캐시는 저비트 표현(예: 2비트 또는 4비트)으로 저장됩니다. 양자화는 토큰 단위 또는 채널 단위로 적용될 수 있습니다.
-
희소성 기반 방법:
KV 캐시 크기를 직접 줄이지 않습니다. 대신, 주의력 행렬 계산을 최적화하여 헤드 또는 레이어에서 패턴을 식별하여 계산해야 할 항목 수를 줄입니다.
-
토큰 드롭:
- 추방 기반: 점수 함수(대부분 수동으로 설계됨)가 각 토큰(또는 캐시 단위)의 중요성을 평가하고, 점수가 낮은 단위는 추방됩니다.
- 토큰 병합(주의 풀 기반): 여러 인접한 캐시 단위를 하나의 단위로 병합합니다. 예를 들어, StreamingLLM에서는 덧셈 기능을 사용하여 캐시 단위를 풀링합니다.
시스템 최적화:
-
오프로드 기반:
전체 캐시는 청크로 나누어지고, 이러한 청크의 대부분은 CPU 또는 디스크 메모리로 오프로드됩니다. 분할된 예비 채우기 동안 가장 관련성 있는 청크만 GPU로 다시 가져옵니다.
-
하드웨어 인식 알고리즘:
Flash-attention 및 Page-attention과 같은 기술은 현대 GPU 아키텍처를 활용하여 메모리 효율적인 주의력 커널을 구현하고, GPU 메모리 사용량의 피크를 줄입니다.
-
더 나은 인프라 설계:
더 효율적인 프로그래밍 언어 및 분산 추론 프레임워크도 장문 맥락 LLM 추론의 효율성을 높일 수 있습니다.
효율적인 장문 맥락 추론을 위한 각 접근법의 장단점에 대한 자세한 비교는 부록에서 확인할 수 있습니다.
추론 공간 복잡도
우리의 관점에서, 기존의 추론 기술은 공간 복잡도를 기준으로 분류될 수 있습니다. $n$을 맥락 길이라고 하고, $c\geq 1$는 상수라고 하겠습니다.
-
$O(n^2)$: 기하급수적 복잡도, 예: 기본 전체 KV 캐시 추론. 이 복잡도는 장문 맥락 추론 시나리오에서 모든 장치에 매우 많은 자원을 소모합니다.
-
$O(c\times n)$: 선형 복잡도, 예: 청크된 예비 채우기를 사용하는 전체 KV 캐시 추론. 이 복잡도는 여전히 메모리 제약이 있는 설정에서 요구가 많으며, 맥락 길이가 길어짐에 따라 KV 캐시 크기가 증가합니다.
-
$O(n/c)$: 상수 감소가 있는 선형 복잡도, 예: 양자화, 희소 주의력 및 대부분의 시스템 최적화. 이 복잡도는 KV 캐시 크기를 크게 줄일 수 있지만, 맥락 길이가 128K 또는 1M 토큰에 이를 때 비현실적이 됩니다.
-
$O(1)$: 상수 복잡도. 이는 토큰 삭제 또는 RNN을 사용하여 달성할 수 있습니다. 고정된 캐시 크기를 사용하는 토큰 삭제는 $O(1)$이고, Mamba 및 RWKV와 같은 RNN도 추론 중에 상수 복잡도를 유지합니다.
장문 맥락 추론 문제를 해결하기 위해, 우리는 $O(1)$ 복잡도를 가진 알고리즘을 설계하는 것을 목표로 하고 있습니다. 우리는 기존의 추방 기반 알고리즘의 정확성을 향상시키기 위한 더 나은 점수 함수를 개발하는 것을 목표로 하고 있습니다. 이 함수를 수동으로 설계하는 대신, 우리는 정확한 점수 함수를 학습하기 위한 훈련 패러다임을 도입합니다.
Locret
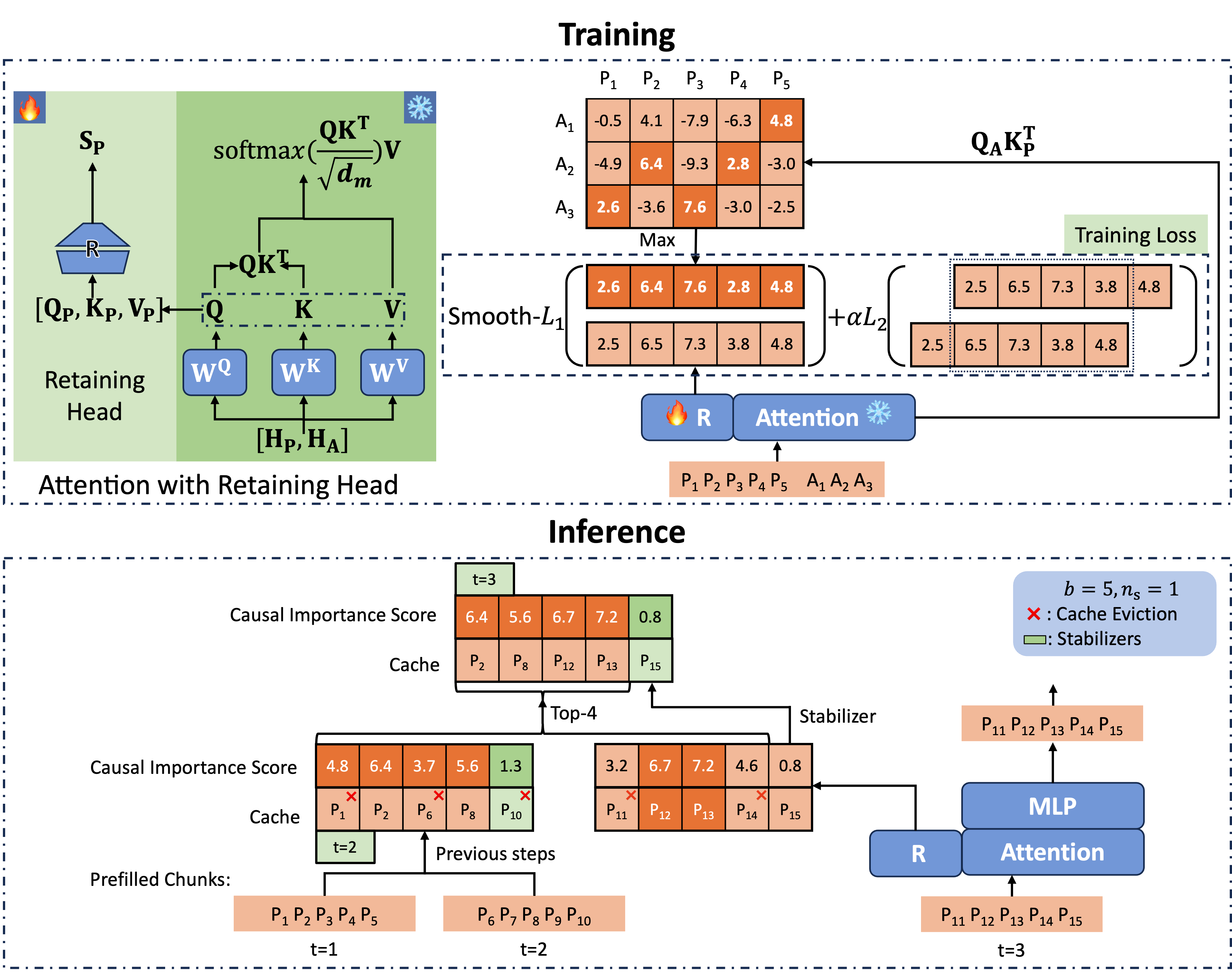
Locret의 전체 프레임워크는 아래와 같이 요약됩니다. 먼저 중요성 점수 함수의 훈련을 진행하고, 그 후 캐시 추방과 분할 예비 채우기가 이루어집니다.
추방을 위한 훈련
Retaining Head 및 인과적 중요성 점수
그림 2에 묘사된 바와 같이, 우리는 각 주의력 모듈에 대해 retaining head(기호로는 $\mathbf{R}$)라는 추가 매개변수를 도입합니다. retaining head는 두 개의 행렬과 비선형 활성화 함수로 구성된 FFN으로 정의됩니다.
\[\mathbf{R}(\mathbf{x}) = \sigma(\mathbf{xW_1})\mathbf{W_2}.\]retaining head의 입력은 $[\mathbf{Q}, \mathbf{K}, \mathbf{V}]$의 연결이며, 이는 KV 헤드 값의 수를 출력하고, 우리는 이를 인과적 중요성 점수(CIS)라고 부릅니다. PyTorch 스타일의 코드 구현은 아래와 같습니다:
cis = self.retaining_head_w2(
self.act(
self.retaining_head_w1(
torch.cat([h_q, h_k, h_v], dim=-1)
)
)
)
정식으로는 다음의 식으로 작성되며, $\mathbf{\tilde S}[k]_j^{(i)}$는 $i$층 $j$헤드에서 $k$번째 토큰의 CIS 점수, 즉 $i$층에서 cis[:, k, j]입니다.
훈련 목표
우리는 다음과 같이 CIS 레이블을 생성합니다. retaining head는 작은 질문-응답 SFT 데이터셋에서 훈련되며, 각 항목은 단일 프롬프트와 하나의 답변으로 구성됩니다. $i$층 $j$헤드에서 $k$번째 토큰의 CIS 레이블은 다음과 같습니다:
\[\mathbf{S}[k]_j^{(i)} := \max_{n_q(d) \leq p \leq n_q(d) + n_a(d)}\left(\mathbf{Q}_j^{(i)}\mathbf{K}_{j}^{(i)T}\right)_{p, k},\]여기서 $n_q(d)$와 $n_a(d)$는 데이터 $d$에서 프롬프트와 답변의 길이를 나타냅니다.
GQA 모델에서 Q와 KV 사이의 헤드 수가 동일하지 않다는 점을 유의하세요. 그래서 우리는 같은 KV 그룹 내의 모든 헤드 중 최대값을 CIS 레이블로 집계합니다.
$L$을 레이어 수로, $h$를 헤드 수로 둡니다. 훈련 목표는 다음과 같습니다:
\[\text{argmin}_{\mathbf{W_1}^{(i)}, \mathbf{W_2}^{(i)}, i=1, 2\cdots, L} \mathbb{E}_{d\in \mathcal{D}}\left[\sum_{i=1}^{L}\sum_{j=1}^{h}\sum_{k=1}^{n_q(d)}\mathcal{L}\left(\mathbf{\tilde S}[k]_j^{(i)}, \mathbf{S}[k]_j^{(i)} \right)\right]\]그리고 손실 함수 $\mathcal{L}$는 다음과 같습니다:
\[\mathcal{L}\left(\mathbf{\tilde S}[k]_j^{(i)}, \mathbf{S}[k]_j^{(i)}\right) = \text{Smooth-}\mathcal{L}_1\left(\mathbf{\tilde S}[k]_j^{(i)}, \mathbf{S}[k]_j^{(i)}\right) + \alpha \mathcal{L}_2\left(\mathbf{\tilde S}[k]_j^{(i)}, \mathbf{\tilde S}[k-1]_j^{(i)}\right),\]여기서 Smooth-$\mathcal{L}_1$는 부드러운 1-노름이고, $\mathcal{L}_2$는 2-노름입니다.
이 방법에 따라 우리는 LongAlpaca에서 3000 스텝 동안 retaining head를 훈련시킵니다. 훈련 시간은 GPU에서 1시간 미만입니다.
Retaining Head를 이용한 추론
이제 우리는 CIS를 예측할 수 있는 정확한 점수 함수를 가지게 되었습니다. 우리는 분할 예비 채우기를 사용하고 예측된 CIS를 기반으로 캐시를 추방합니다.
그림 2에 나와 있는 것처럼, 우리는 성능을 향상시키기 위해 각 레이어와 헤드에서 마지막 $n_s$개의 캐시 유닛을 stabilizers라고 부르며 남겨둡니다. 우리는 고정된 예산 크기 $b$의 캐시 세트를 유지하고, 분할 예비 채우기를 적용합니다. 다음 청크를 처리할 때, 우리는 먼저 CIS를 계산하고 stabilizers에 $+\infty$를 할당한 다음 현재 청크의 캐시와 캐시 세트를 연결합니다. 마지막으로 CIS 점수가 가장 높은 $b-n_s$ 캐시 유닛을 유지합니다. 이 방법은 캐시 세트의 크기가 고정되어 있어 공간 복잡도를 일정하게 유지합니다. retaining head는 정확한 점수를 제공하며, 이후 작업을 위해 가장 중요한 캐시 유닛을 유지합니다. Locret 추론에 대한 의사 코드는 알고리즘 1에 나와 있습니다.

벤치마크: 예산 제한 장문 맥락 추론
성능 벤치마크
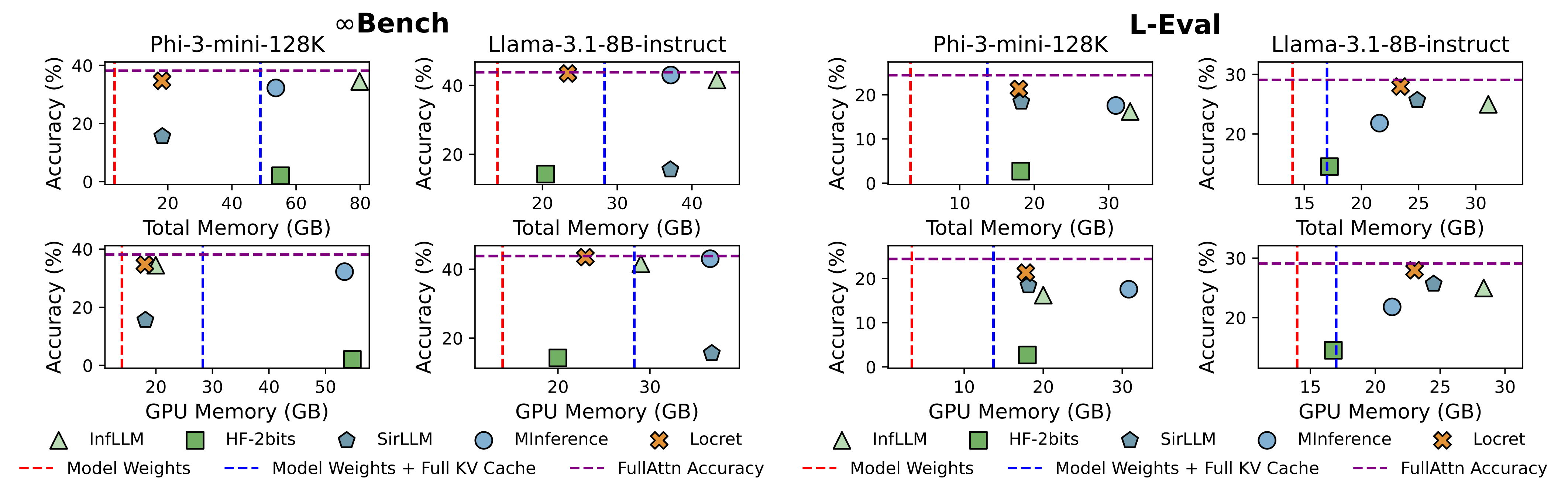
우리는 5가지 기준 방법을 선택하여, 이들 기존 방법과 Locret를 Phi-3-mini-128K 및 Llama-3.1-8B-instruct에서 비교했습니다. Locret의 예산 크기는 각각 6000과 16384로 설정되었습니다. 기준 방법들은 다음과 같습니다:
| 방법 | FullAttn | InfLLM | HF-2bits | SirLLM | MInference |
|---|---|---|---|---|---|
| 범주 | 기본 전체 KV 캐시 | 시스템: 오프로드 | 알고리즘: 양자화 | 알고리즘: 토큰 삭제-추방 | 알고리즘: 희소화 |
결과는 그림 1에 표시되어 있습니다. Locret는 상대적으로 적은 메모리를 사용하면서 가장 높은 벤치마크 점수를 달성했습니다. Locret보다 적은 메모리를 사용하는 방법들은 일부 또는 전체 설정에서 완전히 실패했습니다.
속도 벤치마크
우리는 또한 Locret의 추론 속도를 평가했습니다. 우리는 Nvidia 4090 하나만을 사용하여 모든 기준 방법과 비교했습니다. 이 GPU는 24GB의 메모리만을 가지고 있습니다. 결과는 다음과 같습니다. 일부 방법은 제한된 환경에서 작동하지 않아 입력 맥락을 줄였습니다. 입력 맥락이 OOM 오류를 일으키지 않을 때까지 해당 방법을 실행할 수 있었습니다.
| 모델 | 메트릭 | FullAttn | InfLLM | HF-2bits | SirLLM | MInference | Locret | HF-2bits* | MInference* |
|---|---|---|---|---|---|---|---|---|---|
| Phi-3-mini-128K | tok/s | - | 2276.38 | - | 2352.20 | - | 5080.85 | 1098.51 | 4099.92 |
| Phi-3-mini-128K | 맥락 길이 | 128K | 128K | 128K | 128K | 128K | 128K | 30K | 14K |
| Phi-3-mini-128K | 정확도 | OOM | 99.83 | OOM | 1.69 | OOM | 100.00 | 0.00 | 13.56 |
| Llama-3.1-8B-instruct | tok/s | - | 2287.66 | 1365.51 | 1589.75 | - | 3209.10 | 3680.06 | 5135.74 |
| Llama-3.1-8B-instruct | 맥락 길이 | 128K | 128K | 128K | 128K | 128K | 128K | 30K | 25K |
| Llama-3.1-8B-instruct | 정확도 | OOM | 100.00 | 35.59 | 1.69 | OOM | 100.00 | 26.78 | 20.34 |
양자화 및 토큰 병합과의 정교성
이전 연구에서는 H2O와 같은 추방 기반 방법이 KV 캐시 양자화와 결합될 때 성능이 떨어지는 것으로 나타났습니다. 그러나 Locret는 양자화가 적용되더라도 견고함을 유지합니다.
| 설정 | M | M-4bits | $-\Delta$ |
|---|---|---|---|
| M=FullAttn | 29.08 | 28.52 | 0.56 |
| M=Locret | 27.96 | 27.11 | 0.85 |
Locret에서 양자화로 인한 성능 저하는 전체 주의 방법에서 관찰된 것보다 약간 더 크지만, Locret가 양자화 친화적인 접근 방식임을 나타냅니다.
또한 우리는 추방된 캐시 유닛을 저장할 정적인 크기의 주의 풀을 유지할 수 있습니다. LoCoCo는 H2O에 의해 식별된 비중추 히터에 컨볼루션을 적용하여 이를 달성합니다. H2O를 Locret로 교체함으로써 우리는 두 가지 방법의 결합을 얻게 됩니다.
| 방법 | LoCoCo | Locret | 결합 |
|---|---|---|---|
| L-Eval | 26.01 | 27.96 | 28.70 |
Locret는 LoCoCo보다 더 높은 점수를 달성했으며, 결합된 알고리즘은 두 단독 방법을 모두 능가했습니다. 이는 Locret가 H2O보다 더 정확한 점수 함수를 제공하며, 두 방법이 서로 보완적임을 나타냅니다.
인용
우리의 ArXiV 논문을 참조하십시오.
@article{huang2024locret,
title={Locret: Accelerating Long-Context LLM Inference with Retaining Heads},
author={Yuxiang Huang, Binhang Yuan, Xu Han, Chaojun Xiao, Zhiyuan Liu},
journal={arXiv preprint arXiv:2410.01805},
year={2024}
}
부록
| 범주 | 유형 | 장점 | 단점 | 예시 |
|---|---|---|---|---|
| 알고리즘 | 양자화 | 4비트 이상의 양자화로 성능 손실이 최소화됩니다. 구현이 쉽습니다. | 2비트에서 성능 손실이 큽니다. 추론 속도가 느립니다. 특수 하드웨어가 필요합니다. KV 캐시 크기가 일정하게 줄어듭니다. | KIVI, KVQuant |
| 알고리즘 | 희소화 | 매우 빠른 추론 속도를 자랑합니다. 내부 변수에 대한 GPU 메모리 사용량이 적습니다. | KV 캐시 크기가 줄어들지 않습니다. 더 밀집된 모델(예: MLA, GQA)에서 성능 저하가 눈에 띕니다. | MInference, FastGen |
| 알고리즘 | 토큰 드롭 - 추방 | 빠른 추론 속도와 간단한 구현. 메모리 사용에 제한이 있습니다. | 부정확한 점수 함수로 인해 성능 저하가 발생합니다. | H2O, SirLLM |
| 알고리즘 | 토큰 드롭 - 병합 | 메모리 사용에 제한이 있습니다. | 일부 알고리즘은 추가 훈련이 필요합니다. 사후 훈련이 충분하지 않으면 심각한 성능 손실이 발생할 수 있습니다. | StreamingLLM, LoCoCo |
| 시스템 | 오프로드 | 거의 성능 저하가 없습니다. | 제한된 I/O 대역폭으로 인해 추론 속도가 매우 느립니다. 오프로드 최적화가 필요합니다. | InfLLM, FlexGen |
| 시스템 | 하드웨어 인식 알고리즘 | 높은 하드웨어 활용도, 빠른 추론 속도, 정확도 손실이 없습니다. | KV 캐시 크기가 줄어들지 않습니다. 특정 하드웨어 아키텍처에 맞춘 적응이 필요합니다. | Flash-Attention, Page-Attention |
| 시스템 | 더 나은 인프라 | 기업 수준의 애플리케이션에 적합합니다. | 개발이 매우 어렵습니다. 다양한 시나리오에서 적용 가능성이 제한적입니다. | KTransformers, HexGen |
