Locret: 在个人设备上实现长上下文推理
2024/09 黄宇翔 @清华大学 & 香港科技大学 [English][한국어][にほんご]
简要总结: 我们介绍了 Locret,一种轻量级的基于训练的 KV 缓存压缩方法,利用分块预填充和缓存驱逐。Locret 相比完整缓存,在 Phi-3-mini-128K 和 Llama-3.1-8B-instruct 上分别实现了 $20\times$ 和 $8\times$ 的 KV 缓存压缩比,并且只需要不到1小时的GPU训练时间。Locret 兼容多种高效推理方法,且具有鲁棒性。据我们所知,Locret 是第一个能够在单个 Nvidia 4090 GPU 上部署 Llama-3.1-8B 或类似模型的框架,支持 128K 长上下文推理而不牺牲生成质量,并且只需极少的系统优化。
背景
消费级设备、终端侧LLM 和长上下文推理
近年来,我们见证了大规模语言模型(LLM)的迅速发展。这些模型在几乎所有领域的表现都在不断提升,开发者们现在正致力于为消费级设备设计更紧凑的模型。
消费级设备。 为了提升用户体验,硬件制造商正在设计和生产更便宜、更小的 GPU,或将 GPU 和 NPU 集成到单个 SoC 中,以降低 AI 模型的整体成本。例如,Nvidia 4090 只有 24GB 的 GPU 内存,可以安装在个人电脑中,其价格控制在 2000 美元以下。苹果和高通等公司也在创建针对 AI 计算任务(如矩阵乘法和稀疏操作)优化的设备。然而,这些设备在 GPU 内存和计算能力方面仍然有限。
终端侧LLM。 为了克服内存和计算的限制,终端侧 LLM 被设计和训练用于在用户设备上提供高效的 AI 服务。这些模型的尺寸通常小于 8B,通常在 1B 到 3B 参数之间。MiniCPM 包括从 1.2B 到 4B 的模型,Phi-3-mini 大约为 3B,Llama-3.2 系列有 1B 和 3B 模型。尽管它们的尺寸较小,但这些 LLM 表现出令人印象深刻的能力,常常可以媲美 7B-8B 的模型。为了支持更复杂的任务,如多跳推理、捞针寻宝搜索和 AI 驱动的操作系统,这些模型通常设计为可以处理更长的上下文长度。MiniCPM-3-4B 最多可以处理 32K 的 tokens,而 Phi-3-mini-128K 和 Llama-3.2-1B/3B 甚至支持 128K 的长上下文推理,使得终端侧 LLM 能够有效执行长上下文任务。
长上下文推理。 长上下文 LLM 推理与传统的短上下文推理在两方面有所不同:
-
对注意力机制的计算开销增加
随着上下文长度的增加,计算注意力分数所需的计算量呈二次增长,消耗了每个 transformer 块中的更多计算预算。
-
对键值(KV)缓存的内存需求更高
较长的上下文需要更大的 KV 缓存,显著增加了峰值内存使用量。
这些挑战要求创新技术来降低计算成本并更高效地管理长上下文 LLM 推理中的内存。由于消费级设备的内存有限,无法完全支持如此大的缓存,因此必须开发 KV 缓存压缩算法,使这些设备能够实现长上下文推理,从而实现 LLM 的大众化。
现有的高效推理方法
KV 缓存往往是推理吞吐量的瓶颈,因此开发了几种围绕 KV 缓存的高效推理算法。我们将它们分为算法优化和系统优化。
算法优化:
-
基于量化的方法:
KV 缓存以低位表示(例如 2 位或 4 位)存储。量化可以按 token 或通道进行。
-
基于稀疏性的方法:
没有直接减少 KV 缓存大小。相反,通过识别头部或层中的模式优化注意力矩阵计算,减少需要计算的条目数量。
-
Token 删除:
- 基于驱逐: 评分函数(通常是手动设计的)评估每个 token(或缓存单元)的重要性,分数较低的单元将被驱逐。
- Token 合并(基于注意力池):多个相邻的缓存单元被合并为一个单元,例如在 StreamingLLM 中,使用加法函数来合并缓存单元。
系统优化:
-
基于卸载:
完整缓存被分为多个块,其中大多数块被卸载到 CPU 或磁盘内存中。在块预填充过程中,仅将最相关的块取回到 GPU。
-
硬件感知算法:
类似 Flash-attention 和 Page-attention 的技术利用现代 GPU 架构实现内存高效的注意力核,减少 GPU 内存峰值使用量。
-
设计更好的基础设施:
更高效的编程语言和分散的推理框架也能提升长上下文 LLM 推理的效率。
在附录中可以找到对每种高效长上下文推理方法优缺点的详细比较。
推理空间复杂度
从我们的角度来看,现有的推理技术可以根据它们的空间复杂度进行分类。设 $n$ 表示上下文长度,且 $c\geq 1$ 为常数。
-
$O(n^2)$:二次复杂度,例如原始完整的 KV 缓存推理。这种复杂度在长上下文推理场景中对所有设备都极具资源消耗。
-
$O(c\times n)$:线性复杂度,例如具有块预填充的完整 KV 缓存推理。在内存受限的环境中,这种复杂度仍然很苛刻,因为随着上下文长度的增加,KV 缓存大小也会增加。
-
$O(n/c)$:具有常数减少的线性复杂度,例如量化、稀疏注意力和大多数系统优化。虽然这种复杂度可以显著减少 KV 缓存大小,但当上下文长度扩展到 128K 甚至 1M tokens 时,它变得不切实际。
-
$O(1)$:常数复杂度。通过 token 删除或使用 RNN 可以实现这种复杂度。具有固定缓存大小的 token 删除是 $O(1)$,而像 Mamba 和 RWKV 这样的 RNN 也在推理过程中保持常数复杂度。
为了解决长上下文推理的挑战,我们的目标是设计一种具有 $O(1)$ 复杂度的算法。我们的目标是开发一个更好的评分函数,以提高现有基于驱逐算法的准确性。我们没有手动设计这个函数,而是引入了一个训练范式来学习准确的评分函数。
Locret
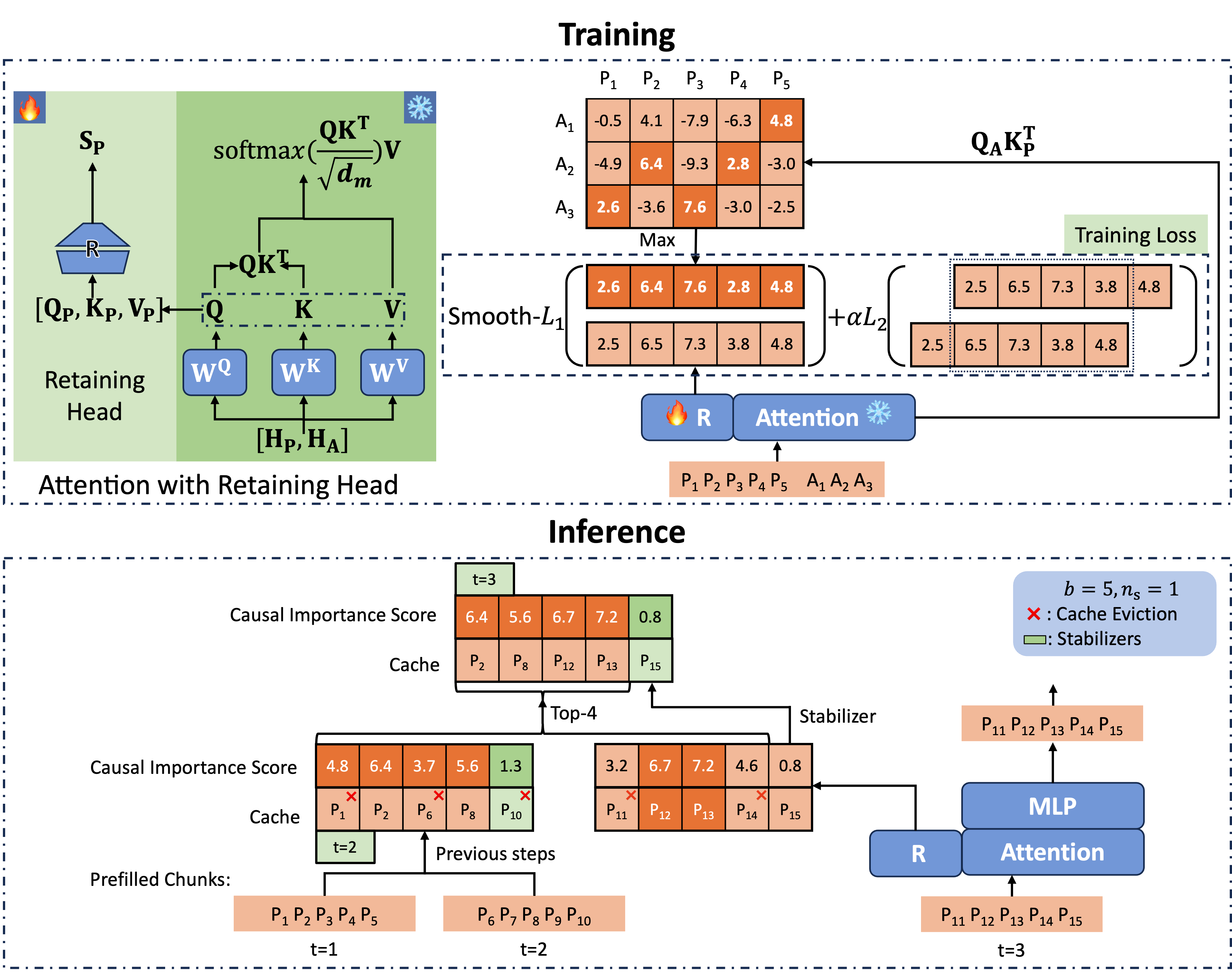
Locret 的整体框架如下所示,我们首先训练重要性评分函数,然后进行缓存驱逐和块预填充。
驱逐训练
Retaining Head 和因果重要性分数
如图2所示,我们为每个注意力模块引入了一个称为 retaining head 的附加参数(记为 $\mathbf{R}$)。retaining head 是由两个矩阵和非线性激活函数组成的 FFN,定义为:
\[\mathbf{R}(\mathbf{x}) = \sigma(\mathbf{xW_1})\mathbf{W_2}.\]retaining head 的输入是 $[\mathbf{Q}, \mathbf{K}, \mathbf{V}]$ 的连接,它输出表示重要性的 KV 头值,我们称之为因果重要性分数(CIS)。以下是 PyTorch 风格的代码实现:
cis = self.retaining_head_w2(
self.act(
self.retaining_head_w1(
torch.cat([h_q, h_k, h_v], dim=-1)
)
)
)
正式来说,这可以写成以下的公式,其中 $\mathbf{\tilde S}[k]_j^{(i)}$ 是第 $i$ 层第 $j$ 头中第 $k$ 个 token 的 CIS 分数,即第 $i$ 层的 cis[:, k, j]。
训练目标
我们生成 CIS 的标签如下。retaining heads 在一个小型的问答微调数据集(SFT)上进行训练,每个条目由一个提示和一个答案组成。第 $i$ 层第 $j$ 头中第 $k$ 个 token 的 CIS 标签为:
\[\mathbf{S}[k]_j^{(i)} := \max_{n_q(d) \leq p \leq n_q(d) + n_a(d)}\left(\mathbf{Q}_j^{(i)}\mathbf{K}_{j}^{(i)T}\right)_{p, k},\]其中 $n_q(d)$ 和 $n_a(d)$ 分别表示数据 $d$ 中提示和答案的长度。
请注意,在 GQA 模型中,Q 和 KV 之间的头数并不相同,因此我们聚合同一 KV 组中所有头的最大值作为 CIS 标签。
设 $L$ 表示层数,$h$ 表示头数。训练目标为:
\[\text{argmin}_{\mathbf{W_1}^{(i)}, \mathbf{W_2}^{(i)}, i=1, 2\cdots, L} \mathbb{E}_{d\in \mathcal{D}}\left[\sum_{i=1}^{L}\sum_{j=1}^{h}\sum_{k=1}^{n_q(d)}\mathcal{L}\left(\mathbf{\tilde S}[k]_j^{(i)}, \mathbf{S}[k]_j^{(i)} \right)\right]\]损失函数 $\mathcal{L}$ 为:
\[\mathcal{L}\left(\mathbf{\tilde S}[k]_j^{(i)}, \mathbf{S}[k]_j^{(i)}\right) = \text{Smooth-}\mathcal{L}_1\left(\mathbf{\tilde S}[k]_j^{(i)}, \mathbf{S}[k]_j^{(i)}\right) + \alpha \mathcal{L}_2\left(\mathbf{\tilde S}[k]_j^{(i)}, \mathbf{\tilde S}[k-1]_j^{(i)}\right),\]其中 Smooth-$\mathcal{L}_1$ 是平滑的 1 范数,$\mathcal{L}_2$ 是 2 范数。
通过这种方法,我们在 LongAlpaca 上对 retaining heads 进行了 3000 步的训练。训练时间少于1GPU时。
使用 Retaining Heads 进行推理
现在我们有了一个能够准确预测 CIS 的评分函数。我们使用分块预填充并根据预测的 CIS 进行缓存驱逐。
如图2所示,我们在每一层的每个头部保留最后 $n_s$ 个缓存单元,称为稳定器,以增强性能。我们保持一个静态预算大小为 $b$ 的缓存集,并应用块预填充。在处理下一个块时,我们首先计算 CIS,给稳定器分配 $+\infty$,然后将当前块的缓存与缓存集合并。最后,我们保留 CIS 分数最高的 $b-n_s$ 个缓存单元。这种方法使空间复杂度保持恒定,因为缓存集具有固定大小。retaining heads 允许准确评分,并保留最关键的缓存单元以进行后续操作。Locret 推理的伪代码如算法1所示。

基准测试:预算受限的长上下文推理
性能基准测试
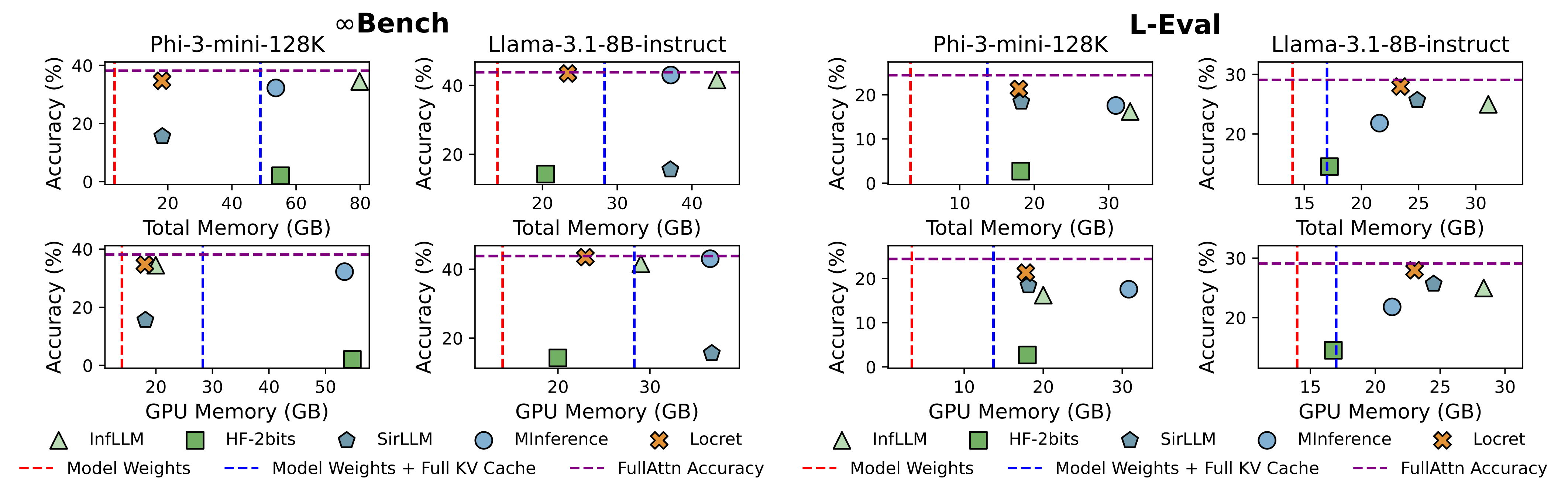
我们选择了 5 种基线方法,它们分别对应现有的方法,并将它们与 Locret 在 Phi-3-mini-128K 和 Llama-3.1-8B-instruct 上进行比较。Locret 的预算大小分别设置为 6000 和 16384。基线方法如下所述:
| 方法 | FullAttn | InfLLM | HF-2bits | SirLLM | MInference |
|---|---|---|---|---|---|
| 类别 | 原始完整 KV 缓存 | 系统:卸载 | 算法:量化 | 算法:Token 删除-驱逐 | 算法:稀疏化 |
结果如图1所示。Locret 在使用相对较少内存的情况下实现了最高的基准分数。比 Locret 使用更少内存的方法在某些或所有设置中都完全失败。
速度基准测试
我们还评估了 Locret 的推理速度。我们将我们的方法与所有基线方法在 单个 Nvidia 4090 上进行比较,该显卡只有 24GB 的 GPU 内存。结果如下。请注意,一些方法在如此有限的环境下无法运行,因此我们截断了输入上下文,直到相应的方法可以运行而不会导致 OOM 错误。
| 模型 | 指标 | FullAttn | InfLLM | HF-2bits | SirLLM | MInference | Locret | HF-2bits* | MInference* |
|---|---|---|---|---|---|---|---|---|---|
| Phi-3-mini-128K | tok/s | - | 2276.38 | - | 2352.20 | - | 5080.85 | 1098.51 | 4099.92 |
| Phi-3-mini-128K | 上下文长度 | 128K | 128K | 128K | 128K | 128K | 128K | 30K | 14K |
| Phi-3-mini-128K | 准确率 | OOM | 99.83 | OOM | 1.69 | OOM | 100.00 | 0.00 | 13.56 |
| Llama-3.1-8B-instruct | tok/s | - | 2287.66 | 1365.51 | 1589.75 | - | 3209.10 | 3680.06 | 5135.74 |
| Llama-3.1-8B-instruct | 上下文长度 | 128K | 128K | 128K | 128K | 128K | 128K | 30K | 25K |
| Llama-3.1-8B-instruct | 准确率 | OOM | 100.00 | 35.59 | 1.69 | OOM | 100.00 | 26.78 | 20.34 |
与量化和 Token 合并的正交性
先前的研究表明,类似 H2O 的驱逐方法在与 KV 缓存量化结合时表现不佳。然而,Locret 即使在应用量化时仍具有鲁棒性。
| 设置 | M | M-4bits | $-\Delta$ |
|---|---|---|---|
| M=FullAttn | 29.08 | 28.52 | 0.56 |
| M=Locret | 27.96 | 27.11 | 0.85 |
量化对 Locret 的性能下降仅略高于完整注意力方法,表明 Locret 是一种量化友好的方法。
此外,我们可以通过应用卷积来存储被驱逐的缓存单元,从而维护具有静态大小的注意力池。LoCoCo 通过将卷积应用于由 H2O 识别的非重击者单元来实现这一目标。通过将 H2O 替换为 Locret,我们得到了两种方法的结合。
| 方法 | LoCoCo | Locret | 组合 |
|---|---|---|---|
| L-Eval | 26.01 | 27.96 | 28.70 |
Locret 的得分高于 LoCoCo,且组合算法优于单独的算法。这表明 Locret 提供了比 H2O 更准确的评分函数,且这两种方法互为补充,展示了它们的正交性。
引用
请引用我们的ArXiV论文.
@article{huang2024locret,
title={Locret: Accelerating Long-Context LLM Inference with Retaining Heads},
author={Yuxiang Huang, Binhang Yuan, Xu Han, Chaojun Xiao, Zhiyuan Liu},
journal={arXiv preprint arXiv:2410.01805},
year={2024}
}
附录
| 类别 | 类型 | 优点 | 缺点 | 示例 |
|---|---|---|---|---|
| 算法 | 量化 | 使用超过 4 位量化时性能损失最小。易于实现。 | 2 位时性能损失显著。推理速度较慢。需要专用硬件。KV 缓存大小恒定减少。 | KIVI, KVQuant |
| 算法 | 稀疏化 | 推理速度非常快。运行时内部变量对 GPU 内存需求低。 | 不减少 KV 缓存大小。在较密集模型(如 MLA、GQA)中性能下降明显。 | MInference, FastGen |
| 算法 | Token 删除 - 驱逐 | 推理速度快,易于实现。内存使用有上限。 | 由于评分函数不准确,导致显著的性能下降。 | H2O, SirLLM |
| 算法 | Token 删除 - 合并 | 内存使用有上限。 | 某些算法需要额外训练。如果后期训练不足,则会造成严重的性能损失。 | StreamingLLM, LoCoCo |
| 系统 | 卸载 | 几乎没有性能下降。 | 由于有限的 I/O 带宽,推理速度非常慢。需要精心的卸载优化。 | InfLLM, FlexGen |
| 系统 | 硬件感知算法 | 硬件利用率高,推理速度快,无准确度损失。 | 不减少 KV 缓存大小。需要针对特定硬件架构进行适配。 | Flash-Attention, Page-Attention |
| 系统 | 更好的基础设施 | 适合企业级应用。 | 开发极其困难。在不同场景中应用性有限。 | KTransformers, HexGen |
